「発想すごい」「どうやって探す?」数学教師が編み出す美しい数式に思わず二度見
同じ数字がずらりと並んだり、繰り返し現れたり…。不思議な数式をTwitterに投稿することで話題なのが、ポテト一郎(@potetoichiro)さん。数字が苦手な人でも見るだけで驚くようなツイートの数々は「美しすぎる」「これ、どうやって見つけるの」と評判を呼んでいる。数学のおもしろさから数式の見つけ方の秘密まで、詳しく話を聞いてみた。

シンプルな式の中に潜む、数字の法則性に驚嘆
社会人になってから幾何に興味を持ち、作問を趣味としていたポテト一郎さん。中学校で数学の教員を務めるかたわら、19年からTwitterで数学に関する投稿を始めた。やがて、不思議な数式や図形のツイートが数学好きを中心に注目を集めていく。いくつか見てみよう(ここで使う「/」は分数の横棒の意味。「/」の左側は分子、右側は分母を示す)。
69854471³-44698544³
=698544716985447169854471-446985444469854444698544
(181818182/18181818182)²=181818182181818182/1818181818218181818182
6⁶1¹4⁴5⁵3³2²8⁸9⁹/9⁹8⁸3³2²5⁵2²6⁶2²4⁴=61453289/983252624
777777/2333332+333333=777777333333/233332
何とも不思議だ。あるいはこんな式もある。
2311686+1762378=4074064
2311686-1762378=549308
2311686×1762378=4074064549308
同じ数字を足した解と引いた解が、掛けたときの解に並んで現れる。さらに難解なものになると、
28815607761506104!9112295268838532!/9112295268838531!28815607761506105!
=288156077615061049112295268838532/911229526883853128815607761506105
この式の中にある「!」は階乗を表す(例えば「4!」は4×3×2×1の意味)。初めて何千ものいいねが付いた数式をブラッシュアップした、ポテト一郎さん会心の作という。さらには、
747×567=423549
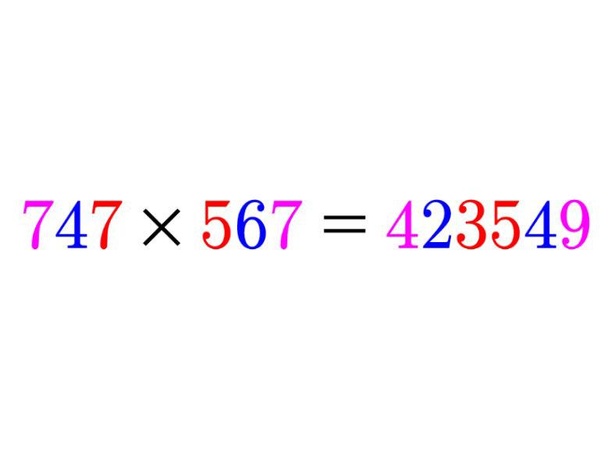
といった式も。何の変哲もない掛け算のように見える。が、よく見ると左辺の747、567の一番外側同士、7と7をかけた49、内側の4、6を掛けた24、最内同士の7、5を掛けた35が、右辺の解に外側からきれいに並ぶように現れる。九九がそのまま解に反映された、レアな数式だ。
シンプルな式の中に潜む数字の法則性の美しさに驚くばかり。それにしても、これらの数式をどうやって見つけているのだろうか。
数式や図形を作るときは、オリジナリティにこだわる
物心ついたころには算数が好きになっていたというポテト一郎さん。数式を見つけるときは、まず「こんな数式があったらいいな」というアイデア、つまり理想形から構想していくという。
「なかなか思うように見つからないことが多く、粘り強くいろいろな方法で考えます。数式をいろいろな形に変形して探したり、コンピュータの力を借りることも。式変形のみで見つかるものでも、かなり桁数が大きな値になる場合はコンピュータの力を借ります。また、完全にコンピュータのみで探すこともあります」
特にこだわるのは、オリジナルの数式を見つけること。「誰も見たことがない数式を探し当てたい、という強い思いがあります。世界は広いので、誰かがすでに発見している場合もありますが」。そんな力作に対する反響には、「数学が好きな方々がリプライ欄のなかで議論されたり、ほかにも似た数式がないか考えて下さったりしてもらえて、とてもうれしいですね」
数式だけではない。数学好きが集う、数学を愛する会主催の「円を3等分する選手権」では、六芒星(星形)を取り入れた極めて斬新な切り方で最優秀賞を獲得。図案でもその独創性を発揮している。
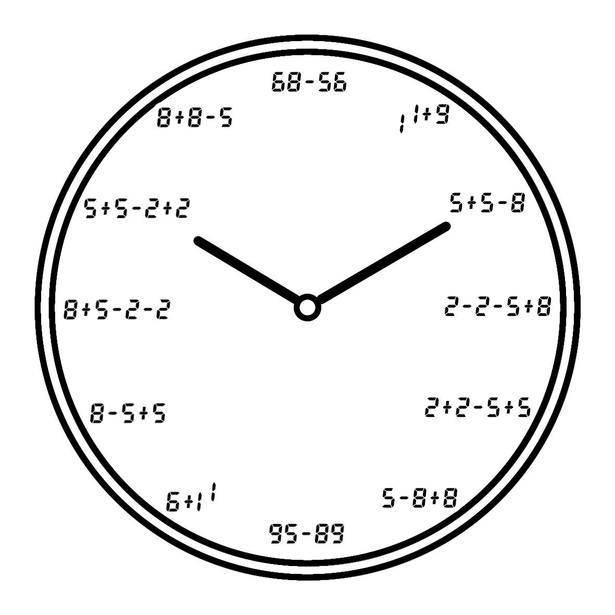
例えば「点対称な時計の文字盤」。この時計の12時の位置には、そのまま12ではなく「68-56」と式で書かれてある。この文字盤をぐるっと180°回転させると、「68-56」は6時の位置でちょうど上下反転するため「95-89」になる。その式を解くと6時の「6」に。これは偶然ではなく、この時計の文字盤1~12がすべて、180°回転させてもぴったり数字が合う式で書かれている。知識がなくても楽しめるのがポテト一郎さんの作品の魅力だ。
数学の魅力は「世界の共通言語である」こと
そんなポテト一郎さんに数学の魅力について聞いてみると、やや意外な答えが返ってきた。「何より素敵なのは、言葉が通じなくても世界中の人たちと数学を使ってコミュニケーションを取れること。年齢、性別も関係ありません」
そもそも一郎さんがTwitterで数式を含む数学関連の投稿を始めたのも、海外で有名な幾何(図形)パズルの作者であるCatriona Agg(@Cshearer41)さんがツイートした幾何の問題を見かけ、その美しさに衝撃を受けたこと。Twitterを始めたころは海外の数学好きを意識して日本語を使わずに投稿、フォロワーは外国人がほとんどだったそうだ。
「アラビア地域からのフォロワーさんが多かったです。アラビア語は読めませんが、それでも解答を送ってもらったりしながらコミュニケーションができました。数学は世界の共通言語なのかな、とも思います」
「不思議な数式の見つけ方」を一つだけ教えてもらったら…
最後に、不思議な数式の見つけ方のなかから比較的簡単だというものを一つだけ教えてもらった。それでもやや難しいが、おもしろいので興味のある方はご覧いただきたい。

(181818182/18181818182)²=181818182181818182/1818181818218181818182
冒頭でも紹介したこの数式の探し方。繰り返し続く「181818…2」に目が行くが、重要ではない。実は「1001」という数字がポイントだ。いきなり、なぜ?と思ってしまうが、1001という数字は、3桁の数字を掛けると同じ数字を繰り返すというトリッキーな性質をもっている(例えば1001に364を掛けると364364になる)。素因数分解するなどして「1001=11×91」と変形。これをベースに桁数を増やしていくと、同じ数字を繰り返す性質を保ったまま
1000000001=11×90909091
100000000001=11×9090909091
という別の数式ができる。これが第1段階。以降、この2つの数式や数字が出てくるので覚えておこう。
さて、ここで出てきた、90909091と9090909091に注目を。前者を後者で割り、さらに2/2を掛けると
(90909091/9090909091)×(2/2)=181818182/18181818182 となる。
さあ、まず 181818182/18181818182 という並びが出てきた。今度はさらにこれを2乗してみる。
(181818182/18181818182)²
=(90909091×2/9090909091×2)²
これを約分して
=(90909091/9090909091)²
=(90909091/9090909091)×(90909091/9090909091)
となる。ここで右の項だけに11/11を掛けて変形する。11/11=1だからそのまま等式で結ばれる。
=(90909091/9090909091)×(90909091×11/9090909091×11)
=(90909091/9090909091)×(1000000001/100000000001)
ほら、ここで第1段階の1000000001、100000000001という数字が出てきた。もう少しだ。さらに計算を進めると
=90909091090909091/909090909109090909091
となり、これに2/2をかけると
=181818182181818182/1818181818218181818182
これで、最初の式
(181818182/18181818182)²=181818182181818182/1818181818218181818182
が完成となる。数式や掛け算、割り算をパズルのように組み合わせて導く楽しみがお分かりいただけただろうか。
「数学はパズル的な部分や不思議な部分が大きな魅力。それを伝えられるようなツイートをしていきたい。自分のツイートを見た人が、見る前よりも、ほんの少しでも数学が好きになってもらえたら、こんなにうれしいことはありません」とポテト一郎さん。次々と編み出される不思議な数式の数々にこれからも注目していきたい。
取材・文=折笠隆


























